本文目录导读:
标题:深度解析“y是x的函数”这一数学概念的内涵与外延
在数学的广阔领域中,函数是一个核心概念,它描述了变量之间的一种特殊关系,当我们说“y是x的函数”时,我们实际上是在表达一种依赖关系,即y的值完全由x的值确定,这一表述看似简单,却蕴含着丰富的数学思想和实际应用,本文将从多个角度深入探讨“y是x的函数”这一表述的深层含义,以及它在数学和现实生活中的应用。
函数的定义与性质
我们需要明确函数的定义,在数学上,函数通常被定义为一个特殊的对应关系,它从一个集合(称为定义域)到另一个集合(称为值域)进行映射,如果对于定义域中的每一个元素x,都存在唯一的元素y与之对应,那么我们就称y是x的函数,这里,“唯一”是关键,它确保了函数的确定性,即对于同一个x值,y的值是唯一的。
函数的性质包括单调性、奇偶性、周期性等,这些性质反映了函数在不同区间上的变化趋势和对称性,有助于我们更深入地理解函数的本质,单调性描述了函数在某一区间内是增函数还是减函数,奇偶性则揭示了函数图像关于原点或y轴的对称性。
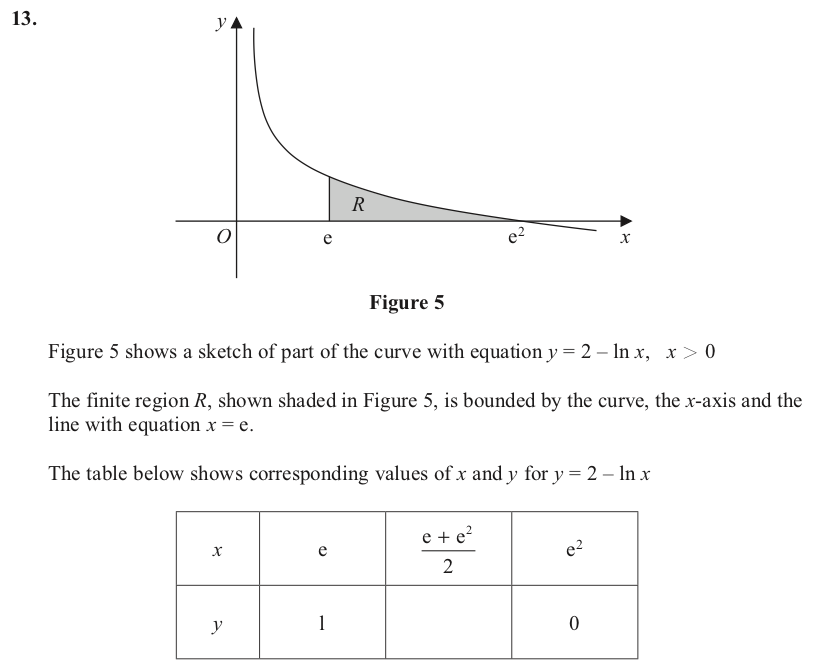
y是x的函数的具体表现
当我们说“y是x的函数”时,实际上是在描述一种变量间的依赖关系,这种依赖关系可以表现为多种形式,如线性关系、二次关系、指数关系等,每种关系都对应着一种特定的函数形式,如线性函数、二次函数、指数函数等。
以线性函数为例,它的一般形式为y=kx+b(其中k和b为常数),在这个函数中,y的值完全由x的值和常数k、b决定,当x取不同的值时,y会按照线性规律变化,这种变化是连续的、平滑的,且在整个定义域内都是唯一的。
除了线性函数外,还有许多其他类型的函数也体现了“y是x的函数”这一概念,二次函数描述了变量之间的抛物线关系;指数函数则描述了变量之间的指数增长或衰减关系,这些函数形式各异,但都遵循着“一个x对应一个y”的基本原则。
函数在现实生活中的应用
“y是x的函数”这一概念不仅在数学领域有着广泛的应用,也在现实生活中发挥着重要作用,许多自然现象和社会现象都可以通过函数关系进行描述和预测。
在自然科学领域,函数被广泛应用于描述物理现象、化学反应和生物过程等,在物理学中,速度、加速度、力等物理量之间的关系可以通过函数进行表达;在化学中,反应速率、浓度等参数的变化也可以通过函数进行描述,这些函数关系不仅有助于我们理解自然现象的本质,还可以为科学实验和工程设计提供理论依据。
在社会科学领域,函数同样发挥着重要作用,在经济学中,需求函数和供给函数描述了商品价格和数量之间的关系;在统计学中,回归函数则用于分析变量之间的相关性和预测未来趋势,这些函数关系有助于我们理解社会现象的发展规律,为政策制定和决策提供科学依据。
函数概念的深化与拓展
随着数学的发展,函数的概念也在不断深化和拓展,现代数学中,函数的定义更加抽象和一般化,可以涵盖更广泛的数学对象和结构,在集合论中,函数被定义为一种特殊的二元关系;在泛函分析中,函数则被视为一种更复杂的数学对象,具有更丰富的性质和结构。
随着计算机科学的兴起和发展,函数的概念也被引入到计算机编程和算法设计中,在计算机程序中,函数通常被用来实现特定的功能或操作,通过输入参数和返回值来实现数据的处理和转换,这种函数式的编程方式有助于提高代码的可读性和可维护性,也有助于实现更高效的算法和数据结构。

总结与展望
“y是x的函数”这一表述不仅揭示了变量之间的依赖关系,还体现了数学的严谨性和确定性,通过深入研究函数的定义、性质和应用,我们可以更好地理解自然现象和社会现象的本质规律,为科学研究和实际应用提供有力支持。
展望未来,随着数学和计算机科学的不断发展,函数的概念和应用将继续拓展和深化,我们可以期待更多新的函数形式和性质被发现和研究,为数学和其他领域的发展注入新的活力和动力,我们也应该注重将函数的概念和方法应用到实际问题中,为解决现实生活中的挑战和问题提供有效的数学工具和手段。
在结束本文之前,我想强调的是,“y是x的函数”这一表述虽然简单,但它所蕴含的数学思想和实际应用却是无比丰富和深刻的,通过不断学习和探索这一领域的知识,我们可以不断提升自己的数学素养和解决问题的能力,为未来的科学研究和实际应用奠定坚实的基础。






发表评论