本文目录导读:
勾股定理:数学史上的璀璨明珠
在数学的广袤领域中,有一个定理以其简洁的形式和深远的内涵,成为了数学史上的璀璨明珠,它就是勾股定理,这个定理不仅在数学领域有着举足轻重的地位,更在物理学、工程学、建筑学等多个领域发挥着不可替代的作用,本文将详细阐述勾股定理的定义、历史背景、证明方法、应用实例以及其在现代科学中的意义。
勾股定理的定义
勾股定理,也被称为毕达哥拉斯定理或商高定理,是一个关于直角三角形的边长的定理,它表述为:在直角三角形中,直角边的平方和等于斜边的平方,如果用a、b表示直角三角形的两条直角边,c表示斜边,那么勾股定理可以表示为a² + b² = c²,这个定理揭示了直角三角形三边之间的数量关系,是数学中最为基础和重要的定理之一。

历史背景
勾股定理的历史可以追溯到公元前约2500年的古巴比伦时期,当时的人们已经发现了一些特殊直角三角形的边长关系,但并未形成系统的定理,公元前6世纪,古希腊数学家毕达哥拉斯及其学派发现了这个定理的一般形式,并将其命名为“毕达哥拉斯定理”,在中国,商高在公元前11世纪就提出了“勾三股四弦五”的特例,这也是中国数学史上最早关于勾股定理的记载。
证明方法
勾股定理的证明方法多种多样,其中最为著名的是欧几里得的证明,他利用相似三角形和面积的概念,通过构造一个正方形和四个相同的直角三角形,巧妙地证明了勾股定理,还有赵爽弦图、总统证法等多种证明方法,每一种方法都展示了数学家的智慧和创造力。
应用实例
勾股定理在日常生活和工程实践中有着广泛的应用,在建筑学中,工程师可以利用勾股定理来计算建筑物的高度、宽度和长度等尺寸,在物理学中,勾股定理被用于计算物体的运动轨迹和速度等物理量,在航海和航空领域,勾股定理也被用于计算航线的长度和角度等参数,在图形设计和计算机图形学等领域,勾股定理也发挥着重要作用。
现代科学中的意义
随着科学技术的不断发展,勾股定理在现代科学中仍然具有重要意义,它作为数学基础定理之一,为数学学科的发展提供了有力支撑,在物理学、工程学、计算机科学等领域中,勾股定理的应用不断拓展和深化,为解决实际问题提供了有力工具,勾股定理所蕴含的几何直观和数学美感也激发了人们对数学和科学的热爱和追求。

结论与展望
勾股定理作为数学史上的璀璨明珠,不仅在数学领域有着举足轻重的地位,更在物理学、工程学、建筑学等多个领域发挥着不可替代的作用,它的简洁形式和深远内涵展示了数学的美妙和力量,未来随着科学技术的不断发展和应用领域的不断拓展,勾股定理将继续发挥重要作用并为我们带来更多的惊喜和发现。
拓展思考
1、勾股定理的推广:除了直角三角形外,勾股定理是否可以在其他类型的三角形或四边形中推广?如果可以推广,那么推广后的定理将具有怎样的形式和性质?
2、勾股定理的证明方法创新:虽然勾股定理已经有多种证明方法但数学家们仍在不断探索新的证明方法,这些新的证明方法可能会带来哪些新的启示和发现?
3、勾股定理在现代科学中的应用拓展:随着科学技术的不断发展新的应用领域不断涌现,在这些新的领域中勾股定理将如何发挥作用?我们如何利用勾股定理来解决实际问题?
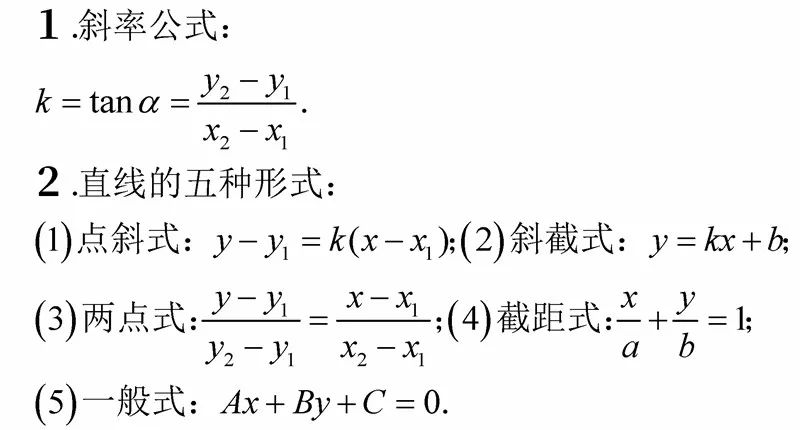
勾股定理作为数学史上的璀璨明珠不仅展示了数学的美妙和力量更在多个领域中发挥着重要作用,通过深入学习和理解勾股定理我们可以更好地掌握数学知识和方法提高解决实际问题的能力,同时我们也可以通过探索勾股定理的推广、证明方法创新以及在现代科学中的应用拓展来不断拓展自己的视野和思维。






发表评论