本文目录导读:
数学的思维导图绘制指南
数学,作为自然科学和社会科学的基础,其知识体系庞大而复杂,为了更好地理解和记忆数学知识,我们可以使用思维导图这一工具来整理和归纳数学内容,本文将详细介绍如何绘制数学的思维导图,帮助读者系统地掌握数学知识。
绘制思维导图的准备工作
1、确定主题:我们需要明确思维导图的主题是“数学”,这有助于我们在后续的绘制过程中保持内容的聚焦和连贯性。
2、选择工具:绘制思维导图的工具有很多,如纸笔、专业的思维导图软件(如XMind、MindNode等)或在线思维导图平台(如百度脑图、MindMeister等),根据个人习惯和需求选择合适的工具。
3、收集资料:在绘制思维导图之前,我们需要收集相关的数学资料,包括教材、参考书、笔记等,这些资料将为我们提供绘制思维导图所需的内容和信息。
绘制思维导图的步骤
1、绘制中心节点
在思维导图的中心位置,绘制一个代表“数学”的节点,这个节点可以是一个简单的图形(如圆形、方形等),也可以是“数学”这个词汇本身。
在中心节点周围留出足够的空间,以便后续添加子节点。
2、添加一级子节点
根据数学的学科体系,我们可以将一级子节点设置为数学的主要分支领域,如代数、几何、数论、概率统计等。
将这些一级子节点均匀地分布在中心节点周围,用线条将它们与中心节点连接起来。
3、添加二级子节点
对于每个一级子节点,我们可以继续添加二级子节点来细化其内容,在“代数”这个一级子节点下,我们可以添加“线性代数”、“多项式代数”、“抽象代数”等二级子节点。
同样地,用线条将这些二级子节点与对应的一级子节点连接起来。
4、添加更多级子节点(如有需要)
如果需要更深入地细化某个领域的内容,可以继续添加更多级的子节点,但请注意保持思维导图的清晰和简洁,避免过于复杂和混乱。
5、添加关键词和注释
在每个节点旁边添加关键词或短语,以简要描述该节点的内容,这有助于我们快速回顾和理解思维导图的内容。
如果需要更详细的解释或说明,可以在节点下方添加注释或链接到相关资源。
6、调整布局和样式
根据个人喜好和需求,调整思维导图的布局和样式,可以改变节点的颜色、形状和大小,以及线条的粗细和颜色等。
确保思维导图的布局合理、美观且易于阅读。
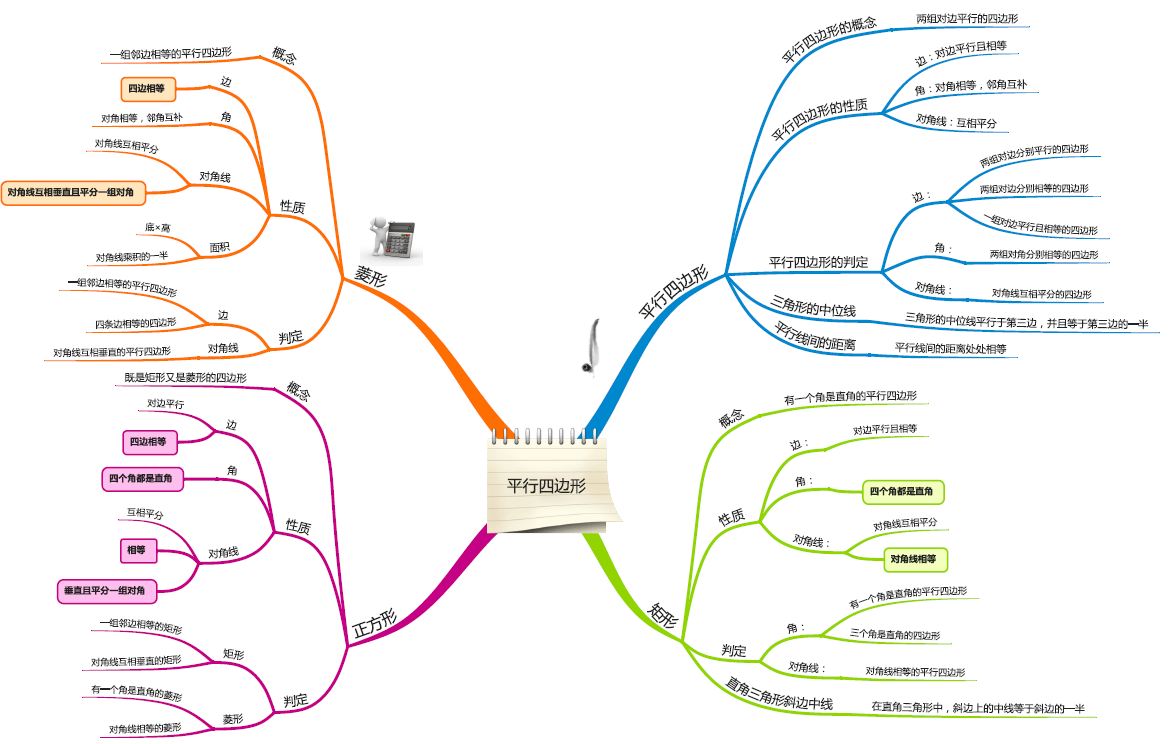
数学思维导图的示例内容
以下是一个简单的数学思维导图的示例内容,供读者参考:
1、代数
线性代数向量、矩阵、线性方程组、特征值与特征向量等
多项式代数多项式运算、因式分解、根与系数的关系等
抽象代数群、环、域、模等
2、几何
平面几何点、线、面、角、三角形、四边形等
解析几何坐标系、直线与曲线、极坐标与参数方程等
立体几何空间图形、体积与表面积等
3、数论
整除与带余除法整除、最大公约数、最小公倍数等
同余与模运算同余式、模运算的性质等
素数与合数素数的判定、素数的分布等
4、概率统计
概率论随机事件、概率的定义与性质、条件概率与独立性等
数理统计总体与样本、统计量、参数估计与假设检验等
通过绘制数学的思维导图,我们可以将复杂的数学知识体系以直观、清晰的方式呈现出来,这有助于我们更好地理解和记忆数学知识,提高学习效率,希望本文提供的思维导图绘制指南和示例内容能对读者有所帮助。